These are the common physical variables and units used in bioprocessing. I know these are quite simple, but since I started this course with barely enough chemistry, physics or maths to pass GCSEs, so I thought it would be useful to write about for any other noobs like me.
*Since I study in the UK my main focus will be on the metric system, but I’ve written some information about converting between them.
Bioprocessing involves a lot of engineering calculations, which in turn involve a lot of manipulation of physical variables. A physical variable can be defined as a physical property of something that can be quantified by measurement (i.e. weight, height, length, etc).
There are 2 types of physical variables:
- Substantial variables
- Natural variables
Lets focus on substantial variables for now. Substantial variables can be attached to units to quantify a measurement. Examples of substantial variables include mass, volume, length, pressure, temperature, time, etc. To express the magnitude of these variables, you need to use precise physical measurements, also known as… Units!
The value of a measurement is split into 2 parts: the number and the unit used for measurement (obviously).
Basic rules:
- You can only add/ subtract substantial variables if they have the same unit. I know this is simple but REMEMBER THIS IN EXAMS. They WILL try to trick you with the units. Always convert all the physical variables into the same units (i.e cm to m, g to kg) before doing the calculation, and ALWAYS DOUBLE CHECK YOUR UNITS ARE CORRECT.
- You can divide/ multiple units to get different physical variables: for example, density is the weight per unit volume, or kg/m³.
SI Units
SI Units are the agreed upon units of measurement used in the U.K., and common throughout the world. There are agreed upon 7 base quantities (substantial variables that cannot not be derived from other variables):

Luminosity and electric current aren’t really important, so you don’t have to worry about those. I’ve only put in the dimensionless symbols so that we can look at derivations of physical variables more easily, you don’t need to remember them.
Little fact: mols and gmol mean the same thing, they are both just moles. I was really confused by this during my first year exams so I thought I’d put it in.
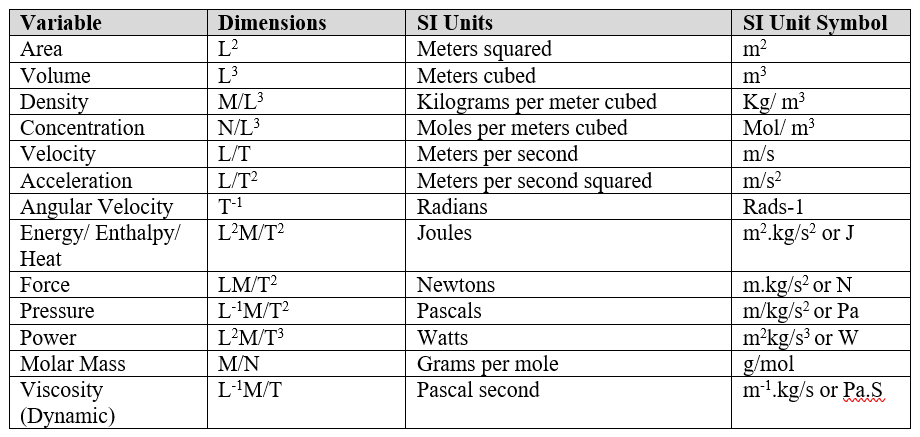
From these 7 base quantities, other physical variables can be derived i.e. speed = L/T or m/s, acceleration = L/T² or m/s². I’ve put a list of all the important derived physical variables you will need to know. I recommend reading and understanding these thoroughly, especially Newtons, Watts, Pascals and Joules as it will help you make sure your answers are correct. Also, if you forget an equation, knowing the units can help you guesstimate what the equation is!
Unit conversions
Most physical variables have multiple units to indicate what the magnitude of the substance is, i.e a kilogram is the same as 1000 grams. Additionally, there are two main systems of measurements: imperial (yards, pints, pounds) and metric (meters, litres, kilograms), and if you decide to move to a different country or are working with a team in another country you will need to be familiar with their unit system. I wouldn’t worry about this since you can just put them into google, though you might get a few questions on your test asking you to convert between systems (if your teacher is especially annoying).
Common Multiplicators
These are prefixes used in front of SI units to indicate the magnitude of the unit; when you see these prefixes use the multiplicator to convert them:
- Kilo (k): 1000x bigger = x10³
- Mega (M): 1,000,000x bigger = x10⁶
- Giga (G): 1,000,000,000x bigger = x10⁹
- Milli (m): 0.001x bigger = x10-³
- Micro (μ): 0.000001x bigger = x10-⁶
- Nano (n): 0.000000001x bigger = x10-⁹
But remember this: A kilometer is 1000x longer than a meter, so there are 0.001 kilometers in a meter. I used to always get this mixed up (yeah I was that behind lol)
Also, when dealing with derived dimensions i.e. density (kg/m³ ), you have to take into account the position of the units. For example, if we want to change m³ to litres (there is 1000 litres in 1 m³), you will have to DIVIDE the density by 1000 since we are looking at the amount of mass per unit volume: if we decrease the volume by 1000 then the mass in that volume will also decrease by 1000. However, if we convert m³ to L, then we will MULTIPLY the value by 1000 since there is 1000 litres per m³ and we are increasing the magnitude of the volume, hence we are counting 1000x more volume. Sorry if this is confusing, I’m finding it hard to explain this concept so please leave a comment if you are confused and I will explain it further or go through some exercises to help you understand.
Unity brackets
I still use unity brackets nowadays – they can be applied to any type of unit conversion and are much more efficient than doing them in your head. It’s quite hard to explain, but I’ll try my best.
Old value x [new SI unit/ conversion rate] = new value.
Basically, you multiply your variable by the conversion rate. The unity bracket should contain the original units and the conversion rate of that unit. For example, if I was converting from grams to kilograms, the unity bracket will have 1 gram and 0.001 kilograms, since 0.001 is the conversion rate of g to kg. The unity bracket should be arranged to allow you to cancel out the old SI unit. Here’s an example of me converting kilograms to grams using it:
2kg x [1000g/1kg] = 2kg x [1000g/1kg] = 2 x 1000 = 2000g.
The unit kg is on the bottom of the unity bracket fraction so that it will cancel out with 2kg. If that’s hard to understand, visualise a 1 underneath the 2kg to present it as a fraction:
2kg/1 x [1000g/1kg]
Here is the use of the unity brackets for converting density. Let’s say we want to convert kg into grams and m³ into litres (dm³):
2kg/m³ x [1000g/1kg] x [1m/ 1000dm]³
2kg/m³ x 1000g/1kg = 2kg/m³ x 1000g/1kg =
= 2 x 1000 = 2000g/m³
[2000g/m]³ x [1m/1000dm]³
= [2000g/m]³ x [1m/1000dm]³
= 2000/1000 = 2g/dm³.
I think this makes more sense? If not, please comment and I will upload more examples + a better definition if possible (I’ve lent my laptop to my friend so I don’t have my own resources right now, but I will by the time this blog gets any attention… if it gets any attention at all). Also, as you see in the example above, if a unit is raised to a power, you must move that power so that the conversion factor is also raised to the same power. This is easier to follow if you make a mistake and makes conversions more simple.
Some common conversion factors between unit systems
I’ve forgotten most of them because we rarely do this at uni, but here are some of the basic ones:
- 1 pound (lb) = 453.6 grams
- 1 kilogram = 2.2 pounds
- 1 inch = 2.54cm
- 1 ft = 30.48cm
- 1 ft = 0.3048m
So if we were to use the unity bracket to convert between kilograms and pounds:
4kg/1 x [1000g/1kg] x [1lb/453.6g]
4kg/1 x [1000g/1kg] = 4kg/1 x [1000g/1kg] = 4 x 1000 = 4000g
4000g x [1lb/453.6g] = 4000g x [1lb/453.6g]
= 4000 / 453.6 = 8.81 lbs
I hope this helps – I’m not the best at describing things (but this blog should help!) so if you have don’t understand it leave a comment and I will try to delve into this topic more and give you more examples.
